前言

本文整理了我在寻求拟合圆的方法中找到的两份matlab代码，内容有参考，将注明出处

（本文若有不正确的地方望大佬们多多指正Orz）

【本文优先发布于我的个人博客网站www.226yzy.com ,转载请注明出处】

最小二乘拟合圆

方法一

​ 当时参考了这份博客的代码(4条消息) 最小二乘圆拟合circfit m sci 代码_diziyue8622的博客-CSDN博客

1. 保存函数

​ 先将下面这份代码保存（保存至默认路径）

1
2
3
4
5
6
7
8
9
10
11
function [xc,yc,R,a] = circfit(x,y)
n=length(x);
xx=x.*x;
yy=y.*y;
xy=x.*y;
A=[sum(x) sum(y) n;sum(xy) sum(yy) sum(y);sum(xx) sum(xy) sum(x)];
B=[-sum(xx+yy) ; -sum(xx.*y+yy.*y) ; -sum(xx.*x+xy.*y)];
a=A\B;
xc = -.5*a(1);
yc = -.5*a(2);
R = sqrt((a(1)^2+a(2)^2)/4-a(3));

保存成功后，调用方式如下

2. 调用函数

​ 首先，我们需要各点的坐标数据，这里为方便演示定义了下面的九组坐标

1
2
x=[1507.2,1484.0,1459.8,1435.6,1410.9,1391.2,1368.5,1350.0,1331.0];
y=[5170.8,5175.4,5176.1,5176.6,5175.1,5191.9,5197.9,5220.3,5240.6];

​ 然后输入下面的代码调用即可

1
[xc,yc,R,a]=circfit(x,y)

3. 参数解读

调用后得到以下结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
xc =
   1.4625e+03

yc =
   5.3278e+03

R =
  156.7942

a =
   1.0e+07 *

   -0.0003
   -0.0011
    3.0500

​ 这里xc和yc分别代表圆心的横坐标和纵坐标，R代表圆的半径，a有三个值分别代表圆的一般方程的三个系数。

​ 这样，通过这种方法就可以得到圆的标准方程或一般方程

4. 绘制

​ 获得拟合后的圆的方程，如果需要绘图，那么我的使用如下代码

1
2
3
4
5
6
7
8
v=xc-R:0.001:xc+R+0.001;
k=sqrt(R.^2-(v-xc).^2)+yc;
k2=-sqrt(R.^2-(v-xc).^2)+yc;
plot(x,y,'b*');
hold on
plot(v,k,'-');
hold on;
plot(v,k2,'-');

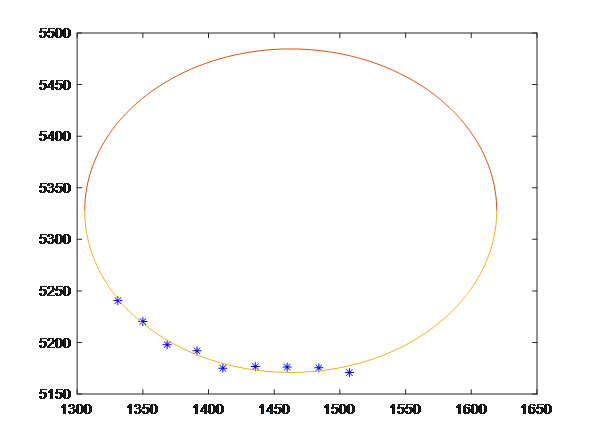
输入成功后你就可以得到绘制的圆，当然这里也许会有一个小问题，就是绘制后的圆因为窗口大小的原因，导致横纵坐标比例不协调，使得圆看起来像椭圆

matlab拟合圆图像变形

​ 对于这种问题，我参考了这个回答matlab怎么控制坐标/画圆形看起来像椭圆怎么办-百度经验 (baidu.com)找到了解决方法，该方法是输入下面的命令

1
axis equal

该命令就是保证横纵坐标轴的最小刻度一致

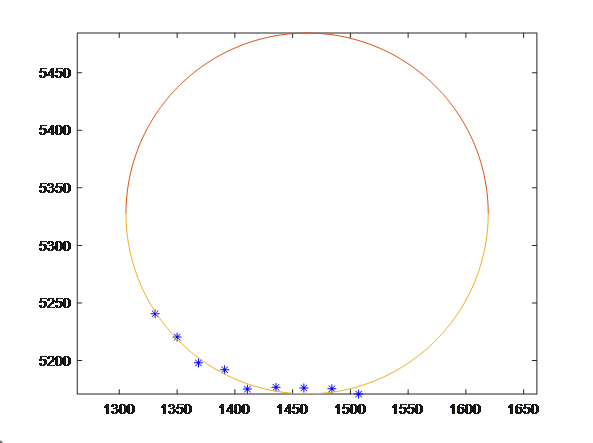
得到的图像如下

matlab拟合圆axis equal图像调整

或者用另一个命令

1
axis square

该命令使横纵坐标比例为1

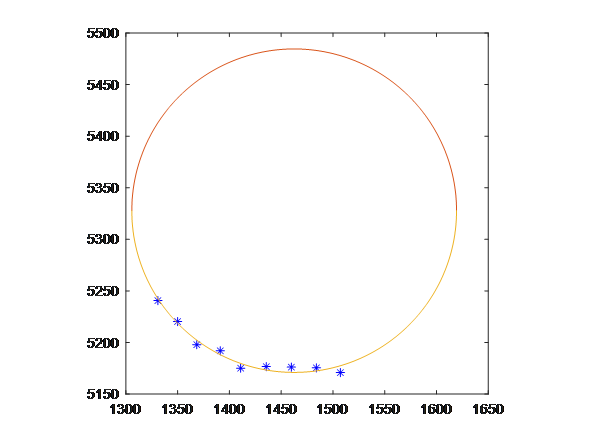
得到的图像如下

matlab拟合圆axis square图像调整

若想恢复默认，只需输入下面的命令即可

1
axis auto

这样你就可以得到一个正常的圆的图像了

方法二

​ 该方法来源于matlab最小二乘法拟合圆 – MATLAB中文论坛 (ilovematlab.cn)中的一个回答

1. 数据与代码

​ 首先还是要有点的坐标数据

1
2
x=[1507.2,1484.0,1459.8,1435.6,1410.9,1391.2,1368.5,1350.0,1331.0];
y=[5170.8,5175.4,5176.1,5176.6,5175.1,5191.9,5197.9,5220.3,5240.6];

下面代码是比较完整的，绘图的部分也有了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ydata = y;
xdata = x;

k0 = ones(1,3);
F = @(k)(xdata-k(1)).^2+(ydata-k(2)).^2-k(3)^2
[k,resnorm] = lsqnonlin(F,k0);

%k(1)是圆心的x坐标
%k(2)是圆心的y坐标
%k(3)的绝对值是圆的半径

r0 = [k(1),k(2)];
R = abs(k(3));
xx = k(1)-R:0.01*R:k(1)+R;
y1_h = sqrt(R.^2 - (xx - r0(1)).^2) + r0(2);
y2_h = -sqrt(R.^2 - (xx - r0(1)).^2) + r0(2);
plot(xx,y1_h,'b')
hold on
plot(xx,y2_h','b')
plot(xdata,ydata,'*r')

当然这个代码也存在方法一中提到图像变形的问题，所以输入

1
axis equal

这样就可以得到一个正常的圆的图像了

2. 参数解读

输入k查询，得到以下结果

1
2
3
k =
   1.0e+03 *
    1.4625    5.3278   -0.1568

前两个值分别代表圆心的横纵坐标，第三个值的绝对值为圆的半径。

输入resnorm查询，得到以下结果

1
2
3
resnorm =

   1.3018e+07

该值根据matlab的中文文档的解释为残差范数的平方（求解非线性最小二乘（非线性数据拟合）问题 - MATLAB lsqnonlin - MathWorks 中国），也就是残差平方和，残差平方和越小，其拟合效果越好。

方法一与方法二得到的拟合圆基本一致